Python library 1.0.x

Technique

Module to create potential waveform and time arrays.

softpotato.technique.Sweep(Eini=-0.5, Efin=0.5, sr=0.1, dE=0.01, ns=2)

Creates the potential and time arrays of a potential sweep. The arguments of this funciton are going to change soon to account for vertexes being different than the initial and final potential. At the moment, final potential refers to the second vertex.

Parameters:

Eini: double, optional
[V], initial potential.
Efin: double, optional
[V], first vertex potential; if Efin > Eini, the first would be positive, negative otherwise.
sr: double, optional
[V/s], scan rate.
dE: double, optional
[V], potential increment
ns: double, optional
number of sweeps. If 1, then the result is a linear sweep.

Returns:

wf: Step instance
the return value is an object with the following attributes:
E: numpy array
[V], potential array
t: numpy array
[s], time array

Examples:

import softpotato as sp
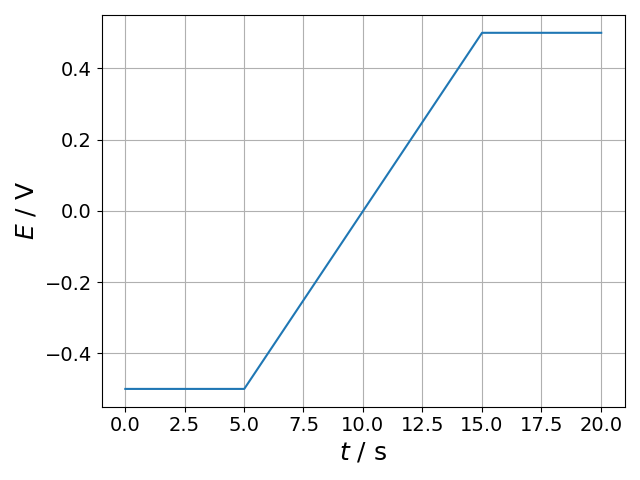
wf = sp.technique.Sweep(Eini=-0.5, Efin=0.5, sr=1, dE=0.01, ns=3)
sp.plotting.plot(wf.t, wf.E, xlab='$t$ / s', ylab='$E$ / V', show=1)

softpotato.technique.Step(Es=0.5, ttot=1, dt=0.01)

Creates a single potential step.

Parameters:

Es: double, optional
[V], step potential.
ttot: double, optional
[s], total time of the step.
dt: double, optional
[s], time step.

Returns:

wf: Step instance
the return value is an object with the following attributes:
E: numpy array
[V], potential array
t: numpy array
[s], time array

Examples:

import softpotato as sp
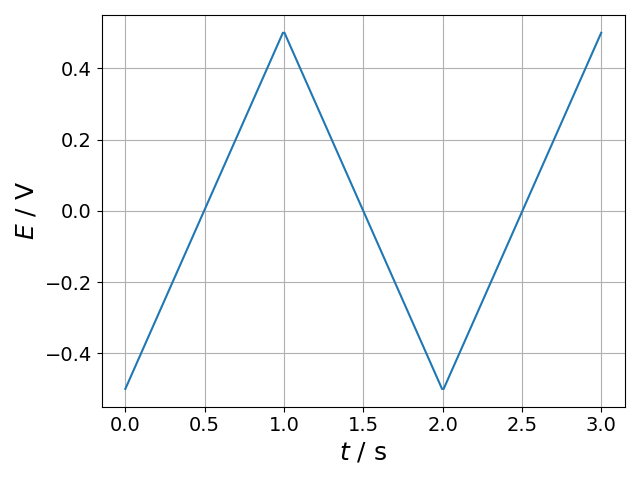
wf = sp.technique.Step(Es=0, ttot=2, dt=0.01)
sp.plotting.plot(wf.t, wf.E, xlab='$t$ / s', ylab='$E$ / V', show=True)

softpotato.technique.Custom(wf)

Combines techniques previously created.

Parameters:

[wf]: list of wf instances
list of potential waveform instances created by potentiostatic techniques (Sweep or Step, see before).

Returns:

wf: Step instance
the return value is an object with the following attributes:
E: numpy array
[V], potential array
t: numpy array
[s], time array

Examples:

import softpotato as sp
wf1 = sp.technique.Step(Es=-0.5, ttot=5)
wf2 = sp.technique.Sweep(ns=1)
wf3 = sp.technique.Step(Es=0.5, ttot=5)
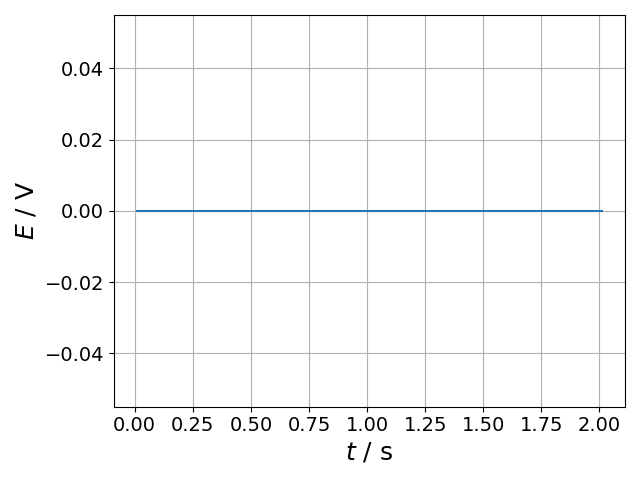
wf = sp.technique.Custom([wf1, wf2, wf3])
sp.plotting.plot(wf.t, wf.E, xlab='$t$ / s', ylab='$E$ / V', show=True)